Maryam Mirzakhani
12 mai 1977 Téhéran – 14 juillet 2017 Standford

Introduction
Maryam Mirzakhani est une mathématicienne iranienne, devenue une icône de la cause des femmes, aussi bien en Iran que partout dans le monde, sans qu’elle l’ait particulièrement cherché.
En effet, c’est la première femme à avoir reçu la prestigieuse médaille Fields, qui est, avec le prix Abel, la plus haute marque de reconnaissance pour un mathématicien (notons qu’il n’y a pas de prix Nobel de mathématiques). La médaille Fields est une récompense attribuée tous les quatre ans à plusieurs mathématiciens ou mathématiciennes (entre deux et quatre), et ce depuis 1936.1
La jeunesse
Maryam est née le 12 mai 1977 à Téhéran, deux ans avant la révolution islamique. Je n’ai pas trouvé grand-chose sur sa famille, ni sur sa vie privée en général. Il apparaît qu’elle protégeait pas mal sa vie privée, autant que faire se peut, mais j’imagine qu’elle est née dans une famille plutôt aisée et en tout cas intellectuelle. Elle a dit de ses parents qu’« ils étaient encourageants et soutenant. C’était important pour eux que leurs enfants aient des professions satisfaisantes et ayant du sens, mais il n’étaient pas particulièrement exigeant sur le succès et la réussite ». Ils sont quatre enfants. Enfant, elle adore lire et écrire des histoires, et veut devenir écrivain. Jeune collégienne, elle ne s’intéresse pas particulièrement aux mathématiques et n’a pas de grande réussite dans cette matière. Mais un jour, son frère lui fait lire la vie de Carl Friedrich Gauss, avec en particulier l’anecdote classique sur sa façon ultra-rapide de calculer 1+2+3+…+100 alors qu’il n’avait que 7 ans, au grand dam du professeur qui croyait avoir donné un calcul suffisamment long pour être tranquille un certain temps. Cela plaît énormément à Maryam, qui se passionne alors pour les mathématiques. Son niveau scolaire atteint très rapidement l’excellence en ce domaine, comme dans tous les autres.
En Iran, en 1976, une organisation nommée SAMPAD (acronyme iranien) ou NODET (acronyme anglais signifiant National Organisation for Development of Exceptional Talents) crée des écoles pour sur-doués (comme on disait à l’époque), dont deux mixtes au passage. Après la révolution islamique l’organisation a continué officieusement, puis a été rétablie officiellement en 1987. L’entrée y est très sélective (test d’intelligence, talent et créativité, plus que connaissances pures) 5 % des gens qui se présentent sont reçus.
Maryam, est douée, très intelligente et créative et est reçue dans un de ces établissements d’excellence, le lycée de jeunes filles Farzanegan à Téhéran, avec sa meilleure amie Roya Behesti. La directrice du lycée pousse les jeunes filles à se dépasser et à oser, comme les garçons. En remarquant les aptitudes particulières de Maryam et Roya en mathématiques, elle les convainc (et convainc les organisateurs?) d’intégrer l’équipe de six élèves pour participer aux Olympiades internationales de mathématiques2. C’est un concours prestigieux réservés aux élèves de moins de 20 ans n’ayant pas encore commencé les études supérieures. En 1994, Maryam remporte une médaille d’or ( elle obtient 41 points sur 42) et Roya une médaille d’argent. Maryam récidive en 1995, et obtient une nouvelle médaille d’or avec la note maximale de 42 sur 42.
Maryam a d’ores et déjà fait preuve de persévérance et d’ambition, et de grande joie à faire des mathématiques. Qualités qui lui seront reconnues ensuite par ses pairs. Non pas ambition dans le sens de pouvoir ou renommée, mais ambition de s’attaquer à des problèmes difficiles. Son amie Roya dit dans un hommage rendu à Maryam par l’American Society of Mathématics,« elle était motivée par la joie et certainement pas par le désir de renommée ou d’influence, et elle a continué à être motivée par la joie même quand elle a reçu renommée et influence ».
Elle est ensuite admise à l’excellente université Sherif de Technologie de Téhéran, toujours en compagnie de Roya, et obtient sa licence en 1999.
En Iran contrairement aux écoles primaires et secondaires, les universités sont mixtes. Et même si depuis les années 90 beaucoup de formes de discriminations envers les femmes existent, ce n’est pas le cas dans le département de mathématiques, où l’ambiance est amicale et décontractée. Roya et Maryam participent avec leurs camarades masculins à beaucoup de compétitions.3
Lors d’un déplacement dans une de ces compétitions, le 17 mars 1998, sur le chemin du retour, le bus dans lequel se trouvent Maryam et ses camarades, fait une embardée et tombe dans un ravin. Ses camarades décèdent, sauf Roya qui est seulement gravement blessée. Elle-même s’en sort sans trop de mal. Cest une grande perte pour les mathématiques iraniennes. J’imagine que vivre un tel évènement vous marque à jamais. On peut conjecturer que cela lui a certainement donner l’envie de voir le bon côté des choses, de ne pas se plaindre et de profiter de la vie. Et profiter de la vie pour Maryam, c’est essentiellement faire des mathématiques.
La thèse aux USA
Cette même année, (avant ou après l’accident?), elle publie une « preuve simple » d’un théorème de Schur, ce qui lui vaut d’être remarquée par l’American Mathematical Society, et lui permettra, entre autres, comme le font tous les brillants cerveaux iraniens, de partir étudier aux USA, à l’université d’Harvard, en compagnie toujours de son amie Roya. Maryam entame une thèse sous la direction du professeur Cart Mc Cullen, lui-même médaillé Fields en 1998. Son professeur la décrit comme « emplie d’une ambition sans peur ». Elle est déterminée, et toujours en questionnement (également deux qualités importantes pour faire des mathématiques).
Elle soutient sa thèse en 2004 qui est considérée comme spectaculaire. En effet, non seulement Maryam a résolu deux problèmes qui résistaient depuis longtemps (chacun d’eux aurait pu faire l’objet d’une excellente thèse) et de plus elle a trouvé des liens inattendus entre ces deux problèmes.
Elle se marie avec un collègue mathématicien tchèque, Jan Vondrák. Elle est nommée maître (ou maîtresse) de conférence à l’Université de Princeton en 2004, puis professeur à Standford en Californie en 2008. Jan et Maryam auront en 2011 une petite fille, Anahita.
Steven Kerchoff, un de ses collègues de Stanford dit d’elle « ce qui est si spécial à propos de Maryam, ce qui la distingue vraiment des autres, c’est l’originalité dont elle fait preuve dans sa façon d’assembler des éléments disparates ».
Un autre de ses collègues, Ralph L. Cohen, quant à lui, dit « Maryam incarnait ce que c’est d’être une personne mathématicienne ou scientifique : essayer de résoudre un problème qui n’a pas encore été résolu, ou de comprendre quelque chose d’encore incompris. Cela nécessite une profonde curiosité intellectuelle. Il y a une grande joie et une grande satisfaction dans chaque pas vers le succès. Maryam était un des très grands esprits de notre temps, et une personne merveilleuse. »
La médaille Fields
Elle obtient en 2014 la prestigieuse médaille Fields, pour « ses contributions exceptionnelles à la dynamique et la géométrie des surfaces de Riemann et de leurs espaces de modules ». Elle devient alors la première femme, et la première iranienne, a obtenir cette récompense, ce qui lui vaut un immense succès, bien au-delà de la communauté mathématique.
Mais comme le disait Roya, elle reste simple et ne souhaite pas être sur le devant de la scène, ni devenir un symbole de la cause des femmes. Elle dit « Je suis sûre que bien d’autres femmes recevront de telles récompenses dans les années à venir ». Elle est également généreuse, et souhaite mettre en lumière ses consœurs mathématiciennes. À chacun de ses déplacements professionnels, dans les congrès par exemple, après sa médaille Fields, elle est assaillie de journalistes. Ses consœurs ont mis en place de dispositif « bouclier Maryam Mirzakhani » : elles entourent la jeune femme et interpellent les journalistes « vous vous intéressez au travail des femmes en mathématiques ? Je peux vous parler de mon travail ». Ce qui permettait à Maryam de s’esquiver discrètement.
Maryam se décrivait elle-même comme une « mathématicienne lente ». Son travail porte sur les surfaces de Riemann, qu’on peut voir comme des « doughnuts » (des tores) ou des bouées, avec plus ou moins de trous. Sur chaque surface, il y a une géométrie particulière.
Voici une citation de Maryam sur la façon dont elle fait des mathématiques :
Je n’ai pas de recette particulière. C’est pour cela que faire de la recherche est un défi et par là-même, passionnant. C’est comme être perdu dans la jungle et essayer toutes les connaissances que l’on peut trouver pour découvrir une nouvelle astuce, et avec de la chance, on peut trouver un chemin pour en sortir.
Elle continue ses brillantes recherches, en collaboration avec Alex Eskin, qu’elle avait rencontré à Princeton. Ils publient ensemble « le théorème de la baguette magique ». En 2016, elle est nommée membre « de l’Académie nationale des sciences » (américaine), ce qui lui vaut les félicitations du président iranien, Hassan Rohani.
Une mort prématurée
Malheureusement, on lui diagnostique un cancer du sein et elle s’éteint le 14 juillet 2017, laissant un grand vide dans la communauté mathématique et dans le cœur de ses amis.
On lui rend un vibrant hommage en Iran, on publie même des photos d’elle les cheveux découverts et courts et chacun sait que les cheveux des femmes sont un symbole politique fort en Iran ! Le président Hassan Rohani (considéré comme modéré) fait son éloge en ces termes :
« La brillance sans précédent de cette scientifique créative et être humain modeste, qui a fait résonner le nom de l’Iran dans les forums scientifiques mondiaux, a été un point culminant pour montrer la grande volonté des femmes iraniennes et des jeunes d’aller sur des chemins qui mènent à la gloire, dans des arènes internationales variées ».
Ses amis la décrivent comme une jeune femme passionnée de mathématiques bien sûr, mais également enjouée, chaleureuse, aimant danser et manger, aimant la vie.
Un jour avant sa mort, elle a publie un post « plus je fais de mathématiques, plus je suis exaltée ».

Son travail continue d’inspirer les chercheurs et les chercheuses du monde entier.
Un symbole féministe
Après sa mort, le débat a été (re)lancé en Iran sur « la citoyenneté matrilinéaire ». En effet, les enfants nés de mère iranienne et de père étranger n’avaient pas la nationalité iranienne. C’est à cause du cas de la fille de Marryam Mirzakhani, Anahita, qu’une loi a été votée, le 12 mai 2019 (le jour de son anniversaire). C’était important pour Maryam que sa fille puisse avoir la nationalité iranienne, qu’elle soit en lien avec ses racines.
Anahita, cela veut dire « source divine de la lumière et du logos, de l’eau et de la fertilité ». C’est le nom d’une ancienne et importante divinité perse.
Que Maryam l’ait voulu ou non, elle est devenu un symbole féministe. Le 12 mai, jour de son anniversaire, est « la journée internationale des femmes en mathématiques ». En 2019, elle a été reconnue par l’ONU-Femmes, comme l’une des sept femmes scientifiques qui ont façonné le monde.
Les six autres sont :
- Tu Youyou, chimiste pharmaceutique chinoise, paludisme.
- Kiara Nirghin, chimiste africaine du Sud, conservation de l’eau.
- Katherine Johnson, mathématicienne américaine, voyages hors de l’orbite terrestre (calculs)
- Marie Curie, physicienne et chimiste polonaise et française, découverte de la radioactivité
- Marcia Barbosa, physicienne brésilienne, recherches sur l’eau
- Segenet Kelemu, phytobiologiste moléculaire, éthiopienne, agriculture et pauvreté
Un prix de 50 000 euros, destinées à de jeunes mathématiciennes en début de carrière, porte son nom et est décerné chaque année. La jeune mathématicienne Hong Wang, qui est à ce jour pressentie pour la médaille Fields 2026 a obtenu ce prix en 2022.
L’astéroïde (321357) Mirzakhani porte son nom.
Il y a un très beau film sur la vie et l’œuvre de Maryam Mirzakhani, mais il n’est pas gratuit. Voici un extrait .
Quelques uns des travaux de Maryam Mirzakhani
Une preuve simple du théorème de Schur.
Le mathématicien Issai Schur,10 Janvier 1875 – 10 Janvier 1941, mathématicien russe ayant travaillé en Allemagne quasiment toute sa vie, a démontré en 1905, que dans l’ensemble des matrices complexes carrées de taille n, à valeurs dans un corps, le nombre maximal de matrices inversibles et commutant deux à deux est E(n2/4)+1. (E(x) désignant la partie entière de x).
Elle a proposé une élégante preuve par récurrence et publié une note dans la revue American Mathematical Society.

Ses travaux de thèse
Dans sa thèse, Maryam montre le résultat suivant :
NS(X,L) ~ CX L6g-6 quand L tend vers + l’infini.
X étant une surface hyperbolique de type g (sans point singulier), L un réel positif, NS(X,L) représente le nombre de géodésiques simples (et fermées) sur X de longueur inférieure ou égale à L.
Ce n’est pas encore clair ?
En gros, les surfaces hyperboliques ressemblent à des doughnuts avec un ou plusieurs trous. Elles sont bornées. Le nombre de trous noté g s’appelle leur genre. On peut aussi voir les trous comme des anses.
Le tore est de genre 1 mais en fait c’est une surface euclidienne.
Les autres sont des surfaces hyperboliques. J’en ai dessiné une avec des singularités (les pointes), mais je ne les considère pas dans la suite. Maryam les a considéré bien entendu.
Ses travaux de thèse
Dans sa thèse, Maryam montre le résultat suivant :
NS(X,L) ~ CX L6g-6 quand L tend vers + l’infini.
X étant une surface hyperbolique de type g (sans point singulier), L un réel positif, NS(X,L) représente le nombre de géodésiques simples (et fermées) sur X de longueur inférieure ou égale à L.
Ce n’est pas encore clair ?
En gros, les surfaces hyperboliques ressemblent à des doughnuts avec un ou plusieurs trous. Elles sont bornées. Le nombre de trous noté g s’appelle leur genre. On peut aussi voir les trous comme des anses.
Le tore est de genre 1 mais en fait c’est une surface euclidienne.
Les autres sont des surfaces hyperboliques. J’en ai dessiné une avec des singularités (les pointes), mais je ne les considère pas dans la suite. Maryam les a considéré bien entendu.

Sur ces surfaces, on peut définir une géométrie, c’est à dire mesurer des angles et des distances, tracer des courbes, et une géodésique c’est une courbe telle que la distance entre deux points soit minimale (par exemple une droite dans le plan euclidien), et fermée. Une géodésique simple ça veut dire qu’elle ne se recoupe pas.

Elle a démontré des résultats très précis, les constantes étant définies, etc .
Cela permet par exemple de répondre à la question :
Si on coupe la surface suivant une géodésique simple fermée, quelle est la probabilité de la couper en deux morceaux ?
Elle s’intéresse aussi aux multicourbes qui sont des réunions de géodésiques simples fermées disjointes, et établit le résultat suivant :

Une de ses idées a été de considérer les surfaces par genre, et non pas chaque surface particulière. En effet, il y a par exemple différents tores, sur les quels on définit des géométries différentes. Mais finalement, cela n’intervient pas dans son raisonnement.
A chaque famille de surfaces d’un genre donné, on associe un espace abstrait, l’espace des modules, dans lequel chaque surface est représenté par un point. Elle a développé des outils pour travailler dans cet espace des modules, y résoudre des problèmes et les transposer dans les surfaces hyperboliques. En particulier elle a pu calculer les volumes de ces espaces (qui peuvent eux aussi être assimilé à des surfaces.)
Le théorème de la baguette magique
Un de ses derniers résultats, en collaboration avec Alec Eskin, mathématicien russe né en 1965, naturalisé américain et grand ami et collaborateur de Maryam, donne une solution au problème suivant :
Si on considère une pièce dont les murs sont entièrement tapissé de miroirs, en partant d’une source lumineuse, pourra-t-on éclairer tous les points de la pièce ? On peut voir le problème aussi comme les trajectoires d’une boule de billard, est-ce que tous les points du billards seront sur la trajectoire de la pièce ?
Bien entendu, cela dépend de la forme de la pièce.
Au départ, ce problème avait été posé par Penrose père et fils, (les quels, ils ont tous scientifiques et incroyables dans la famille…), comme petit problème amusant, à chercher en famille pendant les vacances de Noël, dans le journal New Scientist en 1958.

Dans un polygone dont les angles sont rationnels, on peut démontrer que tous les points sont atteints sauf un nombre fini.
Ce qui est une conséquence du théorème de la baguette magique de Mirzakhani, Eskin et E-M-Mohammadi, 2015) qui dit :
Pour chaque surface de translation, l’adhérence de l’orbite par l’action de GL(2,R) est une sous-variété linéaire de l’espace de module.
On retrouve ce fameux espace des modules. L’idée de la preuve est de faire subir des transformations à la surface, (du genre déplier, copier, coller) ; toutes les surfaces obtenues par ces procédés vivent dans l’espace des modules et le théorème précédent permet de trouver une solution simple et élégante. C’est l’idée encore de transposer le problème dans un autre espace dans le quel on peut facilement le résoudre.
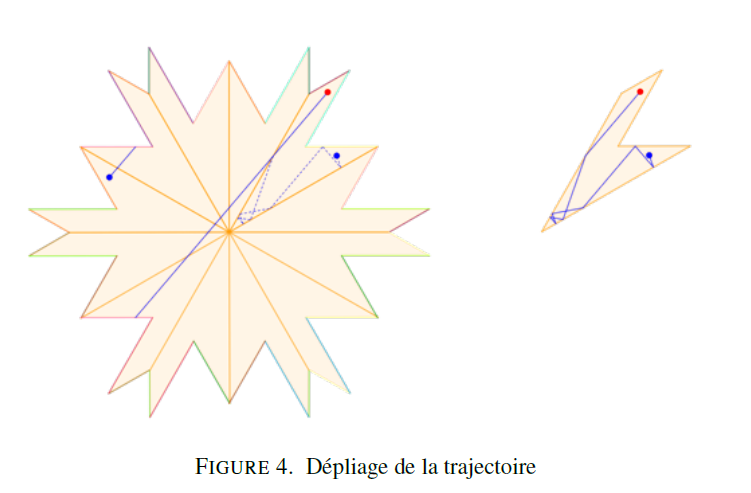
La salle initiale, à droite, est transformée en une salle plus complexe mais où les trajectoires des rayos sont plus simples. On continue les transformations jusqu’à ce que la trajectoire entre les deux points soit une droite. Ces transformations étant réversibles et permettant de trouver la trajectoire du rayon lumineux dans la salle initiale.
Je me suis très largement inspirée des travaux d’Elise Goujard sur Mirzakhani :
L’article suivant ; et la vidéo suivante sur les surfaces hyperboliques.
- La médaille Fields :
Il y a eu en tout (jusqu’en 2022) 62 lauréats et deux lauréates. Pour les lauréates, il s’agit de Maryam Mirzakhani en 2014 et Maryna Viazovska en 2022 (ukrainienne).
Il est à noter que les deux pays qui ont reçu le plus de médailles Fields (14 chacun) sont la France et les USA. Aucune femme dans ces deux pays, ce qui peut sembler paradoxal.
Ce prix est attribué pour un résultat particulier, et obligatoirement avant l’âge de 40 ans. Plusieurs voix parmi les chercheuses (en particulier Nalini Anantharaman, chercheuse française, elle-même ayant un très beau parcours institutionnel), s’élèvent contre cette limite d’âge – qui avait peut-être du sens en 1936 dans un milieu d’hommes – mais qui clairement pénalise les chercheuses, car avant quarante ans elles ont souvent des charges de familles, et la charge mentale n’étant pas -encore- répartie équitablement entre les hommes et les femmes, elles n’ont pas le temps de se consacrer à leur recherche aussi facilement qu’un homme. En tout cas la question se pose. Pourquoi cette limite d’âge d’ailleurs ? ↩︎ - Les Olympiades internationales de mathématiques ont été crées en 1959. Aujourd’hui la plupart des pays y participent, en envoyant une équipe de 6 élèves maximum. Le taux de féminisation est encore très faible 10 à 15 %. L’Iran est devenue première à ce concours en 1998 et reste encore très bien classée.
Comparaison France – Iran depuis 2018 :
2018 : France 6 garçons 0 fille 33ème / Iran 6 garçons 0 fille 19ème
2019 : France 6 garçons 0 fille 25 ème / Iran 6 garçons 0 fille 23ème
2020 : France 5 garçons 1 fille 14ème / Iran 6 garçons 0 fille 18ème
2021 : France 6 garçons 0 fille 27ème / Iran 6 garçons 0 fille 29ème
2022 : France 6 garçons 0 fille 32ème / Iran 6 garçons 0 fille 8ème
2023 : France 6 garçons 0 fille 28ème / Iran 6 garçons 0 fille 11ème
2024 : France 6 garçons 0 fille 21ème / Iran 5 garçons 1 fille 19ème
2025 : France 5 garçons 1 fille 30ème / Iran 6 garçons 0 fille 12ème
On peut noter que l’Iran assure pas mal quand même, mieux que la France en tout cas, et que le taux de féminisation est très faible dans les deux pays, mais comparable. Il est assez représentatif du taux de féminisation général.
https://www.imo-official.org/year_country_r.aspx?year=2024
A titre d’exemple, en 2025, il y a eu 630 concurrents dont 69 filles, soit presque 11 %.
C’est pour remédier à cette disparité, qu’il s’est, paradoxalement, créé des Olympiades féminines.
Pour que les filles prennent leur place, faut-il en passer par des espaces non mixtes ? Apparemment. ↩︎ - Le système scolaire et universitaire iranien est très élitiste, les compétitions sont nombreuses et valorisées. Il peut sembler paradoxal, mais c’est un fait, les jeunes iraniennes sont très éduquées, et majoritaires (60%) dans les études supérieures. Je cite Marjane Satrapi dans Femme, vie, liberté : « Il y a une corrélation mathématique paradoxale entre le rabaissement de la femme iranienne par les mollahs et son haut niveau d’éducation. On leur a dit qu’elle valaient deux fois moins que les hommes. En réaction, elles se sont mises à bosser deux fois plus ».
Dans un article datant de 2014 de la ligue internationale du droit des femmes à propos de Maryam Mirzakhani, on peut lire ceci : « Contrairement aux idées reçues, en Iran, les femmes sont bien plus présentes que les hommes à l’université. Le nombre de femmes admises est passé de40% à plus de 59,9% durant la dernière décennie, alors que le nombre d’élèves (féminins et masculins) est resté le même. Le taux d’obtention de diplômes universitaires, dans deux ou trois ans, sera de plus de 70% pour les femmes. » Ce que confirme Marjane Satrapi en 2023. ↩︎

