Les structures géométriques cachées dans les belles images
Introduction
Un de mes étudiants de l’Isae-Supaéro m’a demandé des clés pour comprendre pourquoi un tableau est beau, harmonieux ou pas. C’est une question qui m’intéresse pour mon propre travail artistique, bien qu’elle ne soit pas du tout « dans l’air du temps » dans l’art contemporain ou dans l’art singulier, pour qui le beau n’est pas un objectif en soi, au contraire.
Moi, la recherche du beau et de l’harmonie ça me concerne. Je serais heureuse à la fin de ma vie si j’ai pu contribuer d’une façon quelconque, infime, à la beauté et l’harmonie dans ce monde, qui en manque pas mal. En revanche, jusqu’à présent, j’ai eu une approche plutôt intuitive face à une œuvre d’art, du style « ça me touche, ça ne me touche pas », et si ça me touche, je rentre plutôt dans un état contemplatif, sans chercher à décortiquer ce qui me plaît ou m’émeut.
Et d’ailleurs, je ne suis pas du tout intéressée par les œuvres artistiques qui nécessitent trois tonnes d’explications, pour les quelles le discours prime sur l’œuvre (comme une banane scotchée sur un mur par exemple). Chacun fait ce qui veut mais moi je m’en fiche comme de ma première paire de chaussettes.
Comme j’ai à cœur de répondre aux questions qu’on me pose si je peux, je me suis mise à faire des recherches.
J’ai découvert qu’à chaque fois, quand un tableau ou une photo paraît belle et harmonieuse, il y a une structure mathématique cachée derrière.
Quelles sont ces structures ?
La règle des tiers
Il y a déjà la basique règle des tiers, encore faut-il la connaître, et j’avoue que jusqu’à très récemment ce n’était pas le cas. (Règle des tiers, à ne pas confondre avec la règle de trois comme il est spécifié dans Wikipedia, ce qui m’a bien fait rire).
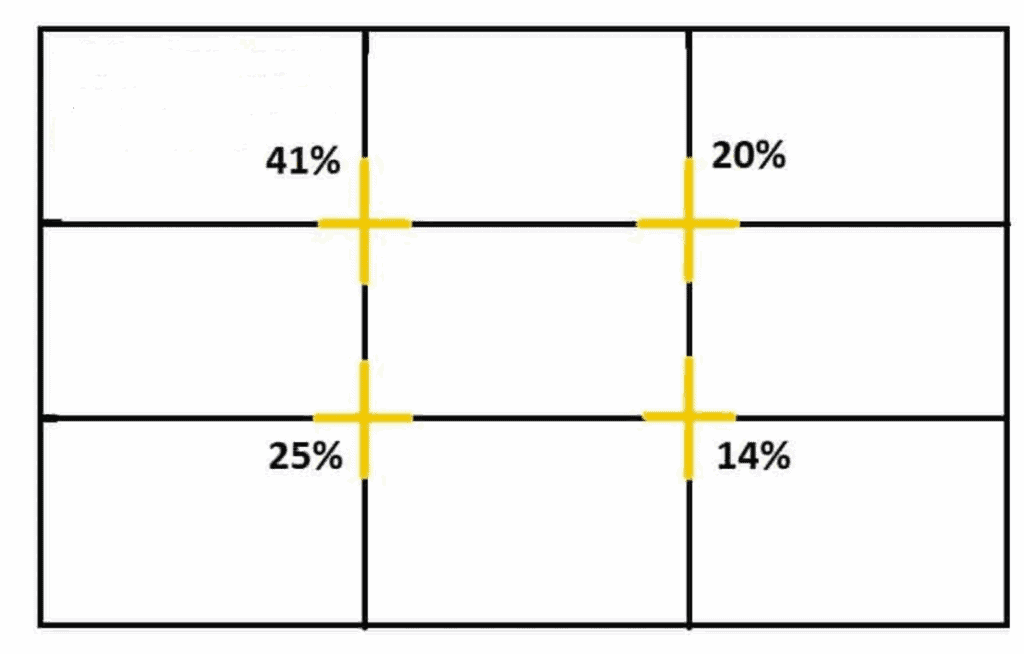
Cette règle consiste à partager l’espace de l’image en 9 rectangles identiques.
Les points d’intersection sont les points sur les quelles le regard va se focaliser (avec des pourcentages différents), les lignes sont les lignes directrices, sur lesquelles placer les éléments structurants, importants de l’image, par exemple les personnages, les lignes d’horizon, les lignes de séparation de plans, etc. C’est une erreur de débutant de placer le sujet central en plain milieu, sauf s’il s’agit d’un portrait en gros plan ou si l’on veut mettre en avant le caractère symétrique de l’image.
Les pourcentages représentent le temps que va passer le regard sur chaque point (du moins pour les personnes qui lisent et écrivent de gauche à droite, sinon c’est l’inverse).
Cela permet aussi de jouer avec les vides et les pleins.
Voici un exemple avec une photo personnelle du port de Marseille, que j’ai cadrée de différentes façons.



Dans la première image, la règle des tiers n’est pas du tout respectée.
Dans la deuxième, la ligne de séparation mer ciel est sur la ligne du bas, le phare et l’oiseau sont sur des points focaux.
Dans la troisième, la règle des tiers est à nouveau respectée, mais la ligne d’horizon coïncide avec la ligne du haut. Cela ne raconte pas la même histoire que la photo précédente.
Voici un autre exemple avec le tableau l’Angélus de Millet, tableau peint entre 1857 et 1859 :

On voit bien que les deux personnages sont sur des lignes verticales, leur visage étant quasiment sur un point focal, et la ligne d’horizon sur une ligne horizontale.
Cette règle est un bon point de départ pour construire quelque chose d’harmonieux.
Les triangles, les cercles et les carrés
Le sujet principal du tableau peut s’inscrire dans une figure géométrique, ce qui donne de la structure et de la tenue au tableau. Souvent, il va s’agir de polygones réguliers, ou de cercle.
Voici quelques exemples :

La madone à la prairie, Raphaël, 1506
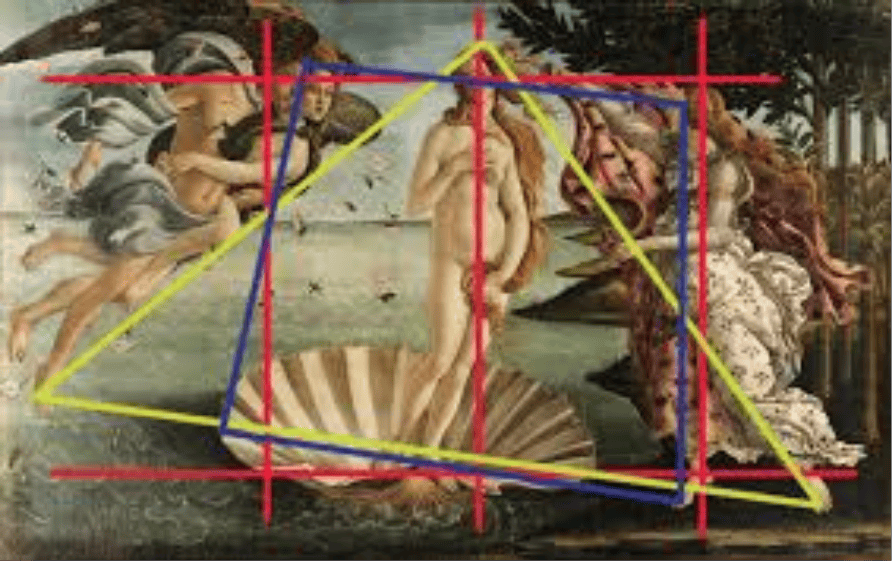
La naissance de Vénus, Botticelli, 1485

La cène, Léonard de Vinci , 1495-1498 (version restaurée)
J’ai représenté quelques unes des structures cachées dans ce tableau, mais il y en a plein d’autres. On peut voir par exemple que les têtes sont toutes dans un même niveau, celle du Christ, le Christ lui même étant isolé dans un cercle, et compris dans un triangle équilatéral. Les personnages sont par groupe de trois de part et d’autre du Christ, à égale distance (non dessiné).
Pour une analyse plus poussée, voir par exemple ici : https://www.bewaremag.com/cene-de-de-vinci-obsede-tant/
Le nombre d’or, la spirale d’or
Le fameux nombre d’or ! Le nombre d’or, souvent noté par la lettre grecque ϕ, vaut très exactement
(1+√5)/2, soit approximativement 1,62, représente « la divine proportion ». C’est à dire, un rectangle est harmonieux si le rapport longueur/largeur vaut ϕ.
Pour une construction exacte à la règle et au compas :
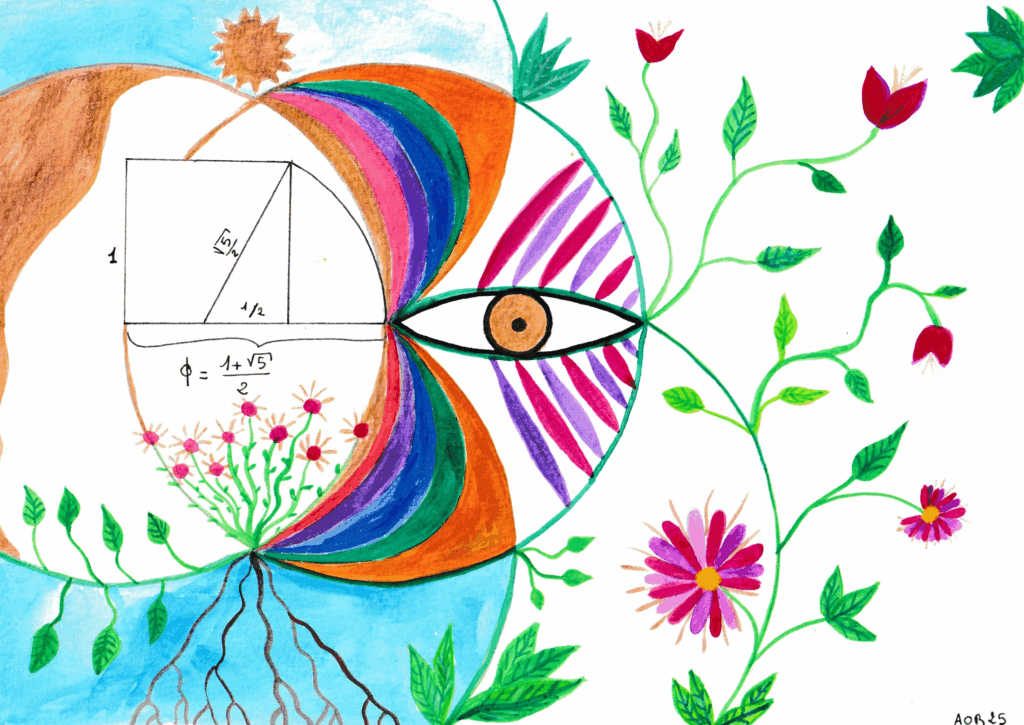
On trace un carré de côté 1, puis on marque le milieu d’un côté. On place la pointe du compas sur ce milieu et l’extrémité sur un des sommets opposés du rectangle, on trace l’arc de cercle (avec le théorème de Pythagore, le rayon vaut √5/2. La longueur tracée est donc exactement ϕ. (Voir figure).
Le nombre d’or est intimement lié aux nombres de Fibonacci. Les nombres de Fibonacci sont les nombres suivants :
1,1,2,3,5,8,13,21,34,55,89, 144,233,377,610,987,1597, Dans cette suite de nombres, chaque nombre (sauf les deux premiers) est obtenu en ajoutant les deux précédents. Le rapport de deux nombres de Fibonacci consécutifs tend vers ϕ. Autrement dit, en construisant un rectangle de côté deux nombres de Fibonacci consécutifs, on obtient un rectangle qui a à peu près les bonnes proportions, pas sûr que la différence soit visible à l’œil nu.
On a 8/5= 1,6 ; 13/8 = 1,62 ; 21/13 = 1,615 ; 34/21 = 1,62. Un rectangle de 34 x 21 fait donc très bien l’affaire.
La particularité d’un rectangle d’or, est que si on trace à l’intérieur un carré de côté la largeur du rectangle, le petit rectangle qui apparaît est exactement un rectangle d’or. C’est même comme cela qu’on définit le nombre d’or. Autrement dit, b/(a-b)=a/b.
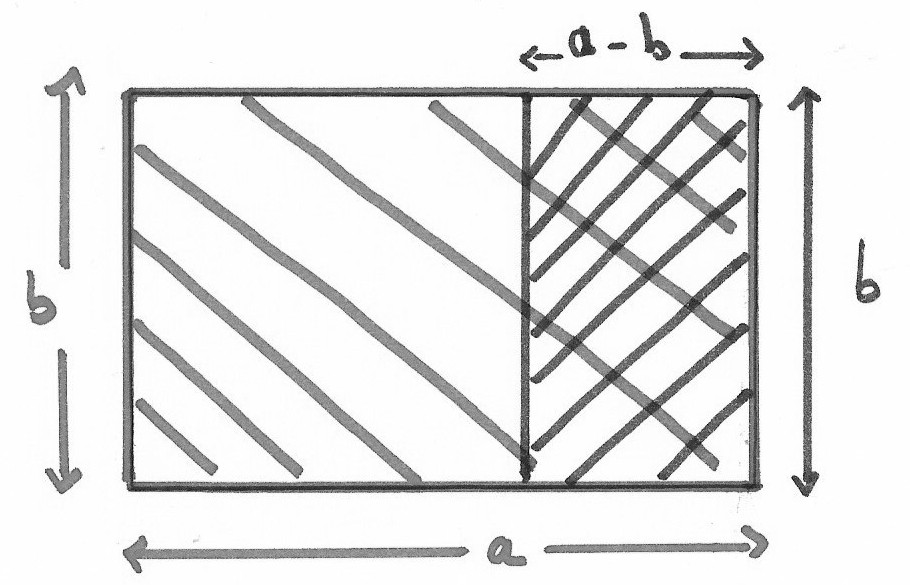
On peut construire des rectangles de Fibonacci, en construisant des carrés emboîtés de côté les nombres de Fibonacci. On voit apparaître des rectangles qui sont tous, « à peu près » des rectangles d’or.
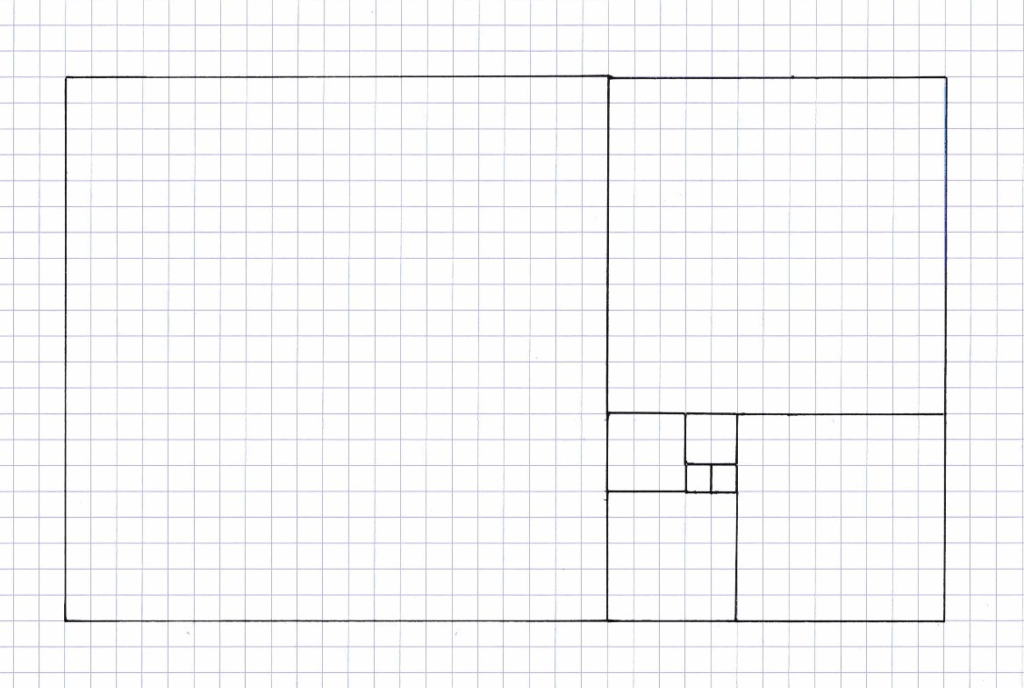
On peut alors tracer une spirale, appelée la spirale d’or ou la spirale de Fibonacci, en traçant les arcs de cercles consécutifs ayant pour diamètre la diagonale du carré.

Ces structures se retrouvent dans beaucoup de tableaux célèbres, et représentent l’harmonie.
Quelques exemples :

La grande vague de Kanawaga, d’Hokuzaï 1830-1831
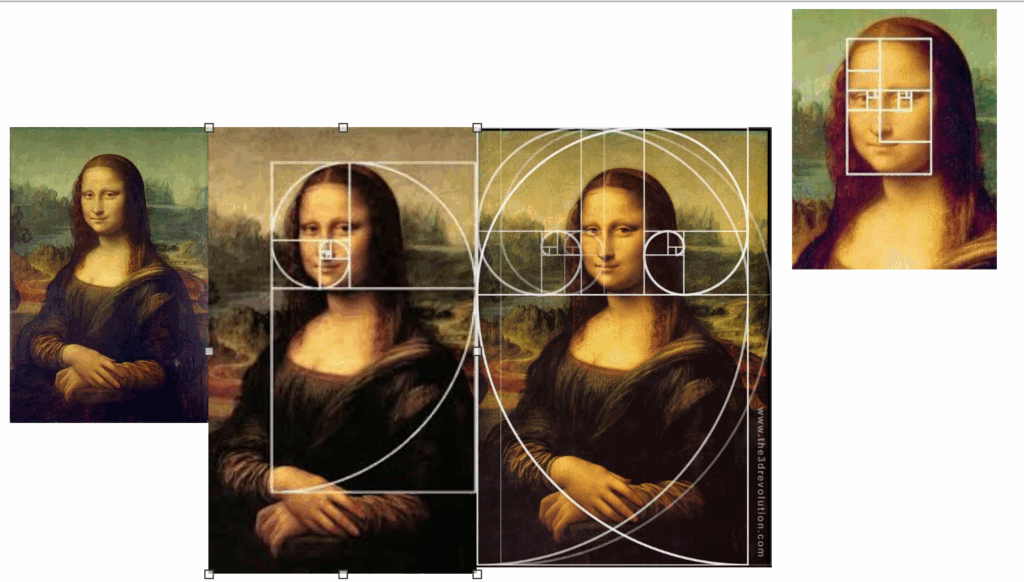
Comme vous pouvez le constater, on retrouve des spirales et des rectangles d’or un peu partout.

